ExamplesA Sandcastle Documented Class Library

This topic contains the following sections.

In Welcome to Sequences, we saw how to represent sequences of natural and odd numbers. In this section, we take a look at a few more complex examples.

For more examples, refer to the functional tests project.

Fibonacci sequence

The Fibonacci sequence is a famous series in mathematics, where each fibonacci number is defined as the sum of the two previous fibonacci numbers, i.e. F(n) = F(n-1) + F(n-2), with seed values F(0) = 0 and F(1) = 1.

In scala, the fibonacci sequence is commonly expressed as follows:

Copy to ClipboardPrint
val fibs: Stream[Int] = 0 #:: 1 #:: fibs.zip(fibs.tail).map { n => n._1 + n._2 }

In C#, the syntax is a little more verbose, but still readable:

Copy to ClipboardPrint
Func<Tuple<int, int>, int> sum = pair => pair.Item1 + pair.Item2;

ISequence<int> fibs = null;

fibs = Sequence.With(0, 1)               //start with (0, 1, ?)
               .Concat(() =>             //and then
                   fibs.Zip(fibs.Tail)   //zip the sequence with its tail (i.e., (0,1), (1,1), (1,2), (2,3), (3, 5))
                       .Select(sum));    //select the sum of each pair (i.e., 1, 2, 3, 5, 8)

The code above creates more objects than needed. The following implementation shows a more efficient way of representing the fibonacci sequence:

Copy to ClipboardPrint
using System.Numerics;

//current and next are any two consecutive fibonacci numbers.
ISequence<BigInteger> Fibs(BigInteger current, BigInteger next)
{
    return new Sequence<BigInteger>(current, () => Fibs(next, current + next));
}

var fibs = Fibs(0, 1);

//prints 0 1 1 2 3 5 8 13 21 34
fibs.Take(10).ForEach(Console.WriteLine);
Prime numbers

One way to find every prime number in a given range is to use the Sieve of Eratosthenes. To find the prime numbers up to 100, a slight variation of the sieve goes like this:

  1. Start with a list representing the range [2, 100].

  2. Let p be the head of the list.

  3. Take p as the next prime number, and remove every multiple of p from the list.

  4. If the list is empty:

    • stop;

    • otherwise, repeat from step 2.

Here's a way of implementing the sieve as a sequence.

Copy to ClipboardPrint
var range = Sequence.Range(2, 101);
var primes = PrimesWithin(range);

//prints: 2 3 5 7 11
Console.WriteLine(primes.Take(5).MkString(" "));            

public ISequence<int> PrimesWithin(ISequence<int> range)
{
    if (range.IsEmpty)
        return Sequence.Empty<int>();

    //take the next prime number 
    var p = range.Head;

    //skip p, and remove further multiples of p 
    var filtered = range.Tail.Where(num => num % p != 0).Force();

    return new Sequence<int>(p, () => PrimesWithin(filtered));
}
Pascal's Triangle

Everyone knows the famous Pascal's Triangle.

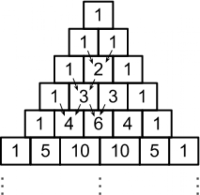
pascals-triangle

The triangle starts with a 1 at the top. In every other row, each number is the sum of the two directly above it.

There are all sorts of ways of representing Pascal's triangle using sequences, but here's an interesting one:

Copy to ClipboardPrint
Func<Tuple<int, int>, int> sum = pair => pair.Item1 + pair.Item2;

Func<ISequence<int>, ISequence<int>> rowFactory =
    row => row.Append(0)                //shift row to the left
              .Zip(row.Prepend(0))      //shift row to the right, and zip both shifted rows
              .Select(sum);             //sum the two shifted rows 

var triangle = Sequence.Iterate(
                            start: Sequence.With(1),
                            func: rowFactory);

You start with row (1). From then on, every row is computed by shifting the row to the right, shifting the row to the left, zipping both shifted rows together and producing the sum of each tuple. For example, given the row (1, 3, 3, 1):

Copy to ClipboardPrint
0 1 3 3 1       //shift right
1 3 3 1 0       //shift left
↓ ↓ ↓ ↓ ↓
1 4 6 4 1
See Also